1006 - 습격자 초라기
본문
초라기는 한국의 비밀국방기지(원타곤)를 습격하라는 임무를 받은 특급요원이다. 원타곤의 건물은 도넛 형태이며, 초라기는 효율적인 타격 포인트를 정하기 위해 구역을 아래와 같이 두 개의 원 모양으로 나누었다. (그림의 숫자는 각 구역의 번호이다.)
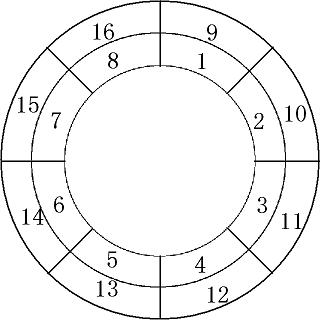
초라기는 각각 $W$명으로 구성된 특수소대를 다수 출동시켜 모든 구역에 침투시킬 예정이며, 각 구역 별로 적이 몇 명씩 배치되어 있는지는 초라기가 모두 알고 있다. 특수소대를 아래 조건에 따라 침투 시킬 수 있다.
- 한 특수소대는 침투한 구역 외에, 인접한 한 구역 더 침투할 수 있다. (같은 경계를 공유하고 있으면 인접 하다고 한다. 위 그림에서 1구역은 2, 8, 9 구역과 서로 인접한 상태다.) 즉, 한 특수소대는 한 개 혹은 두 개의 구역을 커버할 수 있다.
- 특수소대끼리는 아군인지 적인지 구분을 못 하기 때문에, 각 구역은 하나의 소대로만 커버해야 한다.
- 한 특수소대가 커버하는 구역의 적들의 합은 특수소대원 수 $W$ 보다 작거나 같아야 한다.
이때 초라기는 원타곤의 모든 구역을 커버하기 위해 침투 시켜야 할 특수 소대의 최소 개수를 알고 싶어 한다.
입력
첫째 줄에 테스트 케이스의 개수 $T$가 주어진다. 각 테스트 케이스는 다음과 같이 구성되어있다.
첫째 줄에는 (구역의 개수)/2 값 $N$과 특수 소대원의 수 $W$가 주어진다. ($1 \leq N \leq 10000$, $1 \leq W \leq 10000$).
둘째 줄에는 1~$N$번째 구역에 배치된 적의 수가 주어지고, 셋째 줄에는 $N+1$ ~ $2N$번째 구역에 배치된 적의 수가 공백으로 구분되어 주어진다. ($1 \leq$ 각 구역에 배치된 최대 적의 수 $\leq 10000$) 단, 한 구역에서 특수 소대원의 수보다 많은 적이 배치된 구역은 존재하지 않는다. (따라서, 각 구역에 배치된 최대 적의 수 $\leq W$)
출력
각 테스트케이스에 대해서 한 줄에 하나씩 원타곤의 모든 구역을 커버하기 위해 침투 시켜야 할 특수 소대의 최소 개수를 출력하시오.
제한
| 시간 제한 | 메모리 제한 |
|---|---|
| 2sec | 512MB |
- $1 \leq N, W \leq 10000$
풀이
이 문제를 간단한 시각으로 보면 각 방에 특수부대라는 블럭을 채워넣는 문제로 볼 수 있을 것 같다. 각 특수부대는 1개 혹은 2개의 방을 소탕할 수 있으므로, 블럭의 모양은 정사각형 블럭 하나 혹은 그것을 2개 이어붙인 직사각형 모양일 것이다. 문제에서 원하는 해답은 모든 칸을 채워넣을 때 사용한 블럭의 최소 개수이다.
문제만 보면 무조건 dp 방식을 쓸 것처럼 생겼다. 문제는 dp에서는 항상 어떤 상황을 어떤 방식으로 저장해둘지를 정하는게 어렵다는 것… 심지어 방의 모양도 원 모양이라 첫 지점과 끝 지점이 붙어있음을 고려해야한다. 여러모로 골치아픈 경우이다. 그래서 처음에는 방이 원형임을 잠시 잊고, 끝이 이어지지 않은 직사각형 구조로 이해를 시도했다.
첫 시도에서는 현재 위치에 블럭을 채워넣었는지 비워두었는지를 기록하려고 하였다. 그리고, 만약 채워넣었다면 그 블럭이 다른 칸에 어떤 영향을 줄 수 있는지의 상황에 대해 추가적으로 기록하려하였다. 그렇게 만들어진 dp배열은 dp[2][10001][4], 총 8만칸 정도 된다.
그런데 생각해보면 위의 dp배열은 점화식도 이상해지고, 무엇보다 안 쓰는 칸이 너무 많다는 문제점이 있었다. 그래서, 현재 칸에 블럭을 채워넣었는지를 기록하는 방식을 버리려고 하였다. 이 방법으로 dp배열의 크기를 반으로 줄이려고 시도했다. 현재 위치에 추가 블럭을 설치하였는지를 확인하는 기록을 버렸으니, dp배열에는 어떤 의미를 부여해야할까?
과정을 기록하는 것을 포기하였으니, 결과를 기록하는 것으로 노선을 변경해보았다. dp[cur][state] 배열을 만들어, 현재 $\text{cur}$ 위치까지 탐색하고, 현재 상태가 $\text{state}$일 때, 사용한 블럭의 개수의 최솟값을 저장하는 방법을 사용하는 것으로 말이다. 이러면 state가 문제인데, 총 3가지 경우로 나눠질 수 있다. ‘i) 모든 칸이 채워진 경우, ii) 바깥쪽 칸만 채워진 경우, iii) 안쪽 칸만 채워진 경우’ 가 그것이다. 사실 ‘iv) 모든 칸이 채워지지 않은 경우’ 가 더 있는데, 이것은 i) 에서 확인할 수 있는 값이라 무시해도 될 것이다. 그렇게 만들어진 dp배열은 dp[10001][3]의 크기를 가진다. 처음 방법보다 반 이상 크기를 줄일 수 있었다.
무엇을 저장할지 확정하였으니 점화식을 구해보자. 설치할 수 있는 블럭이 2가지밖에 없으므로 설치할 수 있는 조건이 한정적이게 된다. 먼저 안쪽 칸만 채워지는 경우를 찾아보자. 사용할 수 있는 블럭의 모양상 나올 수 있는 경우는 아래 그림 2가지밖에 존재하지 않는다.

바깥쪽 칸만 채워지는 경우 또한 안쪽 칸만 채워지는 경우와 비슷하게 흘러간다. 사용할 수 있는 블럭의 모양상 나올 수 있는 경우는 아래 그림 2가지밖에 존재하지 않는다.

마지막으로 안쪽과 바깥쪽 모두 채워지는 경우이다. 위에서 했던 방식처럼 블럭을 채울 수 있는 경우를 세면 총 5가지가 존재함을 알 수 있다.

이렇게 하면 모든 칸을 채운 dp 배열을 얻을 수 있다. 하지만 방 위치가 선형이 아니라 원형이라는 점이 아직 남아있다. 이 부분에 대해서는 생각을 많이 해봤는데 끝을 어떻게 묶을지 잘 생각이 나지 않았다. 다른 분들의 풀이를 보았는데, 위에서 얘기했던 총 3개의 경우 ( i, ii, iii ) 에서 칸을 강제로 묶을 예정으로 두고, 나머지 방들에 대해 dp를 수행하는 방식으로 구현한 것을 알 수 있었다. 강제로 2칸짜리 블럭을 둘 곳을 정해두고, 그 경우에 맞춰 해답을 찾는 것이었다. 블럭을 놓을 곳의 적의 수를 강제로 $w$로 설정하여 무조건 1칸짜리 블럭만을 두도록 하고, dp 해답에서 강제로 묶은 블럭의 수만큼 빼면 원하는 해답을 찾을 수 있다는 접근법이었다.
- 참고 알고리즘 : 다이나믹 프로그래밍
코드
사용 언어 : C
최종 수정일 : 2023 / 1 / 14
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include <stdio.h>
#define ALL 2
#define OUT 1
#define IN 0
#define MAX_IDX 10001
int cost[2][MAX_IDX];
int n, w;
#define min(a, b) (((a) > (b)) ? (b) : (a))
int getResult() {
int dp[MAX_IDX][3] = {0};
// first case
dp[1][IN] = 1, dp[1][OUT] = 1;
if (cost[IN][1] + cost[OUT][1] <= w) {
dp[1][ALL] = 1;
} else {
dp[1][ALL] = 2;
}
// use dp algorithm
for (int i = 2; i <= n; ++i) {
dp[i][IN] = dp[i - 1][ALL] + 1;
if (cost[IN][i] + cost[IN][i - 1] <= w) {
dp[i][IN] = min(dp[i][IN], dp[i - 1][OUT] + 1);
}
dp[i][OUT] = dp[i - 1][ALL] + 1;
if (cost[OUT][i] + cost[OUT][i - 1] <= w) {
dp[i][OUT] = min(dp[i][OUT], dp[i - 1][IN] + 1);
}
dp[i][ALL] = dp[i - 1][ALL] + 2;
if (cost[IN][i] + cost[OUT][i] <= w) {
dp[i][ALL] = min(dp[i][ALL], dp[i - 1][ALL] + 1);
}
if (cost[IN][i] + cost[IN][i - 1] <= w) {
dp[i][ALL] = min(dp[i][ALL], dp[i - 1][OUT] + 2);
}
if (cost[OUT][i] + cost[OUT][i - 1] <= w) {
dp[i][ALL] = min(dp[i][ALL], dp[i - 1][IN] + 2);
}
if (cost[IN][i] + cost[IN][i - 1] <= w && cost[OUT][i] + cost[OUT][i - 1] <= w) {
dp[i][ALL] = min(dp[i][ALL], dp[i - 2][ALL] + 2);
}
}
return dp[n][ALL];
}
int main() {
int t;
scanf("%d", &t);
while (t--) {
scanf("%d %d", &n, &w);
for (int i = 1; i <= n; ++i) {
scanf("%d", &cost[IN][i]);
}
for (int i = 1; i <= n; ++i) {
scanf("%d", &cost[OUT][i]);
}
// first case : no merge
int retval = getResult();
if (n > 1) {
// second case : IN merge
if (cost[IN][1] + cost[IN][n] <= w) {
int tempA = cost[IN][1], tempB = cost[IN][n];
cost[IN][1] = cost[IN][n] = w;
retval = min(retval, getResult() - 1);
cost[IN][1] = tempA, cost[IN][n] = tempB;
}
// third case : OUT merge
if (cost[OUT][1] + cost[OUT][n] <= w) {
int tempA = cost[OUT][1], tempB = cost[OUT][n];
cost[OUT][1] = cost[OUT][n] = w;
retval = min(retval, getResult() - 1);
cost[OUT][1] = tempA, cost[OUT][n] = tempB;
}
// last case : IN OUT merge
if (cost[IN][1] + cost[IN][n] <= w && cost[OUT][1] + cost[OUT][n] <= w) {
cost[IN][1] = cost[IN][n] = w;
cost[OUT][1] = cost[OUT][n] = w;
retval = min(retval, getResult() - 2);
}
}
printf("%d\n", retval);
}
return 0;
}
solve(): 현재 상황에 맞는 dp 알고리즘을 실행하는 함수cost[][]: 입력으로 주어지는 각 방에 있는 적들의 수를 기록dp[][]: dp 알고리즘 진행값을 기록
